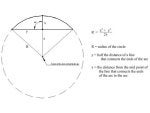
I have some objects that contain arcs that I would like to duplicate. Let me clarify, it is the arcs, the gentle, sweeping curves, that I would like to duplicate. My problem is that I don't know of a way to determine the radius of the existing arc other than make a tracing then break out a compass and start guessing.
So, is there some formula or method that folks use to determine the arc radius? Other than trial and error, which I'll do if necessary.
Thanks
Bill W
So, is there some formula or method that folks use to determine the arc radius? Other than trial and error, which I'll do if necessary.
Thanks
Bill W