angles for this table base

rjherald · Nov 16, 2017

I could use some assistance on figuring the angles for this table base. the length is scaled down a bit from the plans but the angle thing is giving me fits. plans call for a 20 degree angle on the long cross brace. will this angle be the same if the table is shorter that the plans? i do remember trig but this has got me baffled. the short pieces that complete the X call for a 50 degree angle on the center and 20 degree on the other end. i attached a picture of what i am working on. thanks for the assistance

rjherald

wormil · Nov 16, 2017

If you find the vertical center it should be two isosceles triangles which will simplify things, won't even need Pythagoras.

Lazyman · Nov 16, 2017

Unless you scale the height and length by the same percentage, the angles will change. Is this something you have already built or is this a picture of what you are going to build? If you already built it, then you may be able to use a rafter square to figure out one of the angles using rise/foot. Since these appear to be isosceles triangles, then you can figure out all of the other angles using that one angle because the sum of the angles of a triangle = 180 degrees.

You haven't said why you need the angle. How exact do you need it?

wormil · Nov 16, 2017

I think he's trying to place the 2 short pieces of the X brace (blue in my sketch). You don't actually need to measure anything. The angles will be the same, you just need to find the vertical center (horizontal dotted line) to get the length. Here is a crude sketch, you have one side of the triangle, all you need to do is find the center and mirror it.

Loren · Nov 16, 2017

I think drawing up a dimensioned drawing
in Sketchup would be worth the time. The
program will give you the angles.

wormil · Nov 16, 2017

I meant to say, you don't need to calculate anything. Naturally you need to measure length.

Honestly you could probably have cut both diagonals full length and half lapped them together in less time than it would take to fuss with short pieces.

Lazyman · Nov 17, 2017

I guess I am being a little dense (or my inexperience is showing). I don't see how to get the correct angles with lengths alone. If you know the angle of the bottom right joint and make that cut first, then I could see that knowing the lengths of both sides would allow you to mark a cut line but if you don't know either one, it seems like there would be an infinite combinations of angles (on both ends) that would match the lengths? That is what I assume is his dilemma? What am I missing?

Here is a calculator that computes angles based upon known dimensions without using trig yourself. I chose SAS (side-angle-side) in my experiment using 90 degrees as the angle where the sides are the height of the trestles and the distance between them. For example, using 36" tall and 72" apart, yields an angle where the diagonal hits the trestle of 26.565°. The problem with this is that it doesn't take into account the thickness of the board so even this yields an inexact result and might not be any help at all. I am sure that their is a carpenters shortcut for this.

jdh122 · Nov 17, 2017

You have two right-angle triangles. On both of them, sides a and b are the height of the side pieces and the length of the piece along the bottom. Use Pythagoras to get the length of the hypotenuse and simple trig to get the angles at the top and bottom of the side pieces. With that determined, subtract 2x the angle at the bottom of the side pieces from 180 to get the angle at which the two pieces meet in the middle.

wormil · Nov 17, 2017

An isosceles triangle has two sides that are the same. He already has one cross piece done so he knows the angles where it joins the table, all he needs is the length of the shorter braces and angle of the vertex. Basically just use the table itself to find what you need to know. Probably simpler to make another long diagonal, hold it in place and strike your lines to find the angle of the vertices and length of the brace. Use a bevel gauge to transfer the angle if using electric saws. It's one of those things that takes longer to explain than do. Just try to imagine how Roy Underhill would do it, but with less bleeding.

Loren · Nov 17, 2017

plans call for a 20 degree angle on the long cross brace. will this angle be the same if the table is shorter that the plans?

- rjherald

No.

Lazyman · Nov 17, 2017

Yeah, that's his problem as I interpret it. He has adjusted the width and needs to figure out what all of the angles are now. Using the link I provided above, it is easy enough to compute the angle from corner to corner but that is not the exactly angle that is needed for a 2×4 because the width of the board changes it slightly and if you want tight, exact joints, I would think that you want the angles to be pretty close to exact.

Hammerthumb · Nov 17, 2017

It s one of those things that takes longer to explain than do. Just try to imagine how Roy Underhill would do it, but with less bleeding.

- Rick_M

That's funny Rick!

jerryminer · Nov 17, 2017

I could use some assistance on figuring the angles for this table base.

- rjherald

Are you still here? Many of us would be happy to figure the angles for you if you give us the dimensions:

1. Distance between leg assemblies
2. Height of table base
3. Thickness of diagonal braces

As Loren said, SketchUp makes this easy

Lazyman · Nov 17, 2017

LOL, there has to be an "easy" way to calculate the angles but sometimes modeling turns out to be the easiest way.

I just realized that the original 20° & 50° angles in the OP can't be right to begin with. If the angle in the original design where it hits the side trestle is 20° then the middle angle would have to be 40°.

wormil · Nov 17, 2017

I guess I am being a little dense (or my inexperience is showing). I don t see how to get the correct angles with lengths alone. - Lazyman

It's because you're obsessing over knowing the angle in degrees when in that number isn't important. It doesn't matter if it's 20°, 22.5°, 34.7°, or something else. Numbers and measurement systems are ways of communicating information. He doesn't need to communicate it just reproduce it once so he can get away with marking it directly on the workpiece. All he needs to do is create a second cross brace identical to the first, hold it in place and mark the angles. If he needs to transfer those angles to a miter saw or miter gauge, he can use a bevel gauge.

To elaborate a minute, different measurement systems can exist because they are only ways of describing a set of conditions that you need to communicate or maybe just remember for your own purpose. You can measure a board in inches or centimeters and give that length to someone far away. Metric/inch is just a matter of preference. Or you can create a story stick and preserve the exact measurement without ever assigning an arbitrary number to the distance. In this case, he doesn't need the numbers, he only needs to reproduce the angle and length of the short crossbraces once. Intuitively you know all this but we become accustomed to working with measurements and it becomes habit.

edit; I hope I don't sound like an asshole, that's not my intention. I used to think in terms of measuring everything but have learned there are other ways of doing things.

wormil · Nov 17, 2017

The guy replied in a different thread for some reason and his new pictures don't include the original crossbrace so if he didn't have that, it makes all my replies moot. Sure would be nice if someone who asked a question would interact with people trying to help so they don't waste their time. I'm out. Good luck.

rjherald · Nov 17, 2017

to rick…

i apologize for reposting in a new topic. i am new to the forum thing and did not mean to make you angry. i dont have a picture of the original crossbrace because i have not cut it yet.

rjherald

wormil · Nov 17, 2017

I don't mean to sound angry. There is a crossbrace in the picture you posted yesterday going diagonally from top left to bottom right but in your new post, that crossbrace is missing. I realize now the picture is not what it appeared and I was answering the wrong question. It would have been nice to know sooner.

rjherald · Nov 17, 2017

the pict i posted is the one i am building. the first pict is one that came from Pinterest. sorry for the confusion

rjherald

Lazyman · Nov 17, 2017

LOL. I still want to know an easy way to compute the angles.

jerryminer · Nov 17, 2017

LOL. I still want to know an easy way to compute the angles.

- Lazyman

invtan (Rise/Run) = angle

Lazyman · Nov 17, 2017

LOL. I still want to know an easy way to compute the angles.

- Lazyman

invtan (Rise/Run) = angle

- jerryminer

Unfortunately, that only works well for a line with no dimensions. The numbers for the rise over run formula are only known for a line that connects the corners but the board in this case doesn't do that. At bottom end of the board, the bottom edge is in the corner, but at the top, the top edge of the board is in the corner. So the angle for the line that you can easily calculate with the rise-run is actually a line that runs diagonally through the board and doesn't represent the angle you actually need to cut to get the precise width and height and have the beveled ends flat against the sides. Does my explanation make sense? It would be easier to show what I mean with a diagram.

Edit: another way to say this that the thickness of the board changes the angle.

I understand that you can get pretty close by scribing lines as Rick described. I just want to know how someone would calculate it. It's probably the old computer programmer in me but I like to have a way to verify that the cut I'm going to make is going to precisely result in the dimensions I'm shooting for.

wormil · Nov 17, 2017

There are several threads on this, the math is deceptively complicated for the reason you gave earlier. The first time I saw this question, it seemed simple until I tried it. If starting from scratch, it is easier to make a mock up from cardboard or draw it. I thought he had already figured out one leg and needed to find a length for the smaller braces. The one X leg table I built, I tacked the braces together with a nail, spread them to the right angle and marked my angles perpendicular to the floor.

From another discussion. I haven't tried this.

Let B be the angle (initially unknown) the leg makes with the floor.
Let T be the thickness of the leg stock.
Let W be the width of outer sides of the X.
Let H be the height of the top of the X from the floor (i.e. the height of the under side of the table top.)
And let F be the width of the foot of the X legs (i.e. the length of the diagonal cut across the leg stock.)

Then sin(B) = T/F (looking at the triangle made by the foot and the thickness)
and
sin(B) = H / sqrt((W - F)^2 + H^2) (looking at the triangle the whole leg makes with the floor.)

Setting the two right sides equal and solving for F, (yeah, it s a mess) will let you compute the angle B (arcsin(T/F)). Then the angle you want is 180 - 2B. (Remember to convert arcsin(T/F) to degrees first.)

Just for reference (and to check my typing skills)

F =( (2T^2W) +/- sqrt((4T^4W^2)-4(T^2-H^2)) )/ 2(T^2-H^2)

(I told you it was a mess.)

- GeBeWubya

JBay found this calculator, but I haven't tried it.

The math is over my head, Sketchup, it only takes a few minutes.
I did find this, (if it works) There is a calculator on the right side you can try.
http://jsfiddle.net/h1xda7qm/

- jbay

jerryminer · Nov 17, 2017

Unfortunately, that only works well for a line with no dimensions.

- Lazyman

Yes, I get what you're saying. The rise/run formula is best for line figures where the board thickness does not come into play.

The "easy way" for me is SketchUp-but you could also do a full-size drawing and copy the angles from the drawing--or, as Rick suggested, take the angles directly from the work.

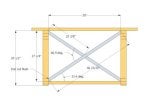
Here is a Sketchup drawing I did based on the OP's info-with some assumptions on my part. He said his "leg height" is 29-1/2", but in the pic it looks like the bottom stretcher is off the floor by 3/4" and the diagonal brace is above the bottom stretcher. Given that, I produced this:

But this would expose part of the brace at the bottom (where noted)-- so I would probably adjust my cuts a little to set the brace a little lower, as in this alternative-which requires a "double cut" at the bottom end of the brace:

If anyone tries to build from this, remember that the angle scale on a miter saw (or a table saw miter gauge) is 90 degrees off from the actual geometry. That is, a "0" cut on a miter saw cuts a 90 degree angle; A "2 degree" setting results in an 88 degree angle. Likewise, to get the 66.9 degree angle in the above drawing, the saw would be set at 23.1 degrees.

The 33.4 degree angle in the drawing would be made with a 33.4 degree setting, as that angle is already calculated from the complementary angle-not the angle of the cut. Confusing, I know, but don't blame me-- blame the guy that decided how to set up the first miter gauge scale. Everybody since has followed his lead.

Lazyman · Nov 18, 2017

Jerry, I went through a similar exercise in Sketchup hoping that I would have a eureka moment on a easy way to calculate the angle. It actually took me a couple of tries to figure out the easiest way to even draw it to get it exact. One of the nice things about using Sketchup is that once you have it drawn correctly, you can use the scale tool to adjust the dimensions and the angles automatically adjust.

Rick, For some reason, I didn't think to search LJ for that. So the short answer is there is no "easy" way to compute it. I may have to plug this into a spreadsheet and see if I can get it to give me the same answer I get in Sketchup.

Thanks guys. Now I know that the universe still has 4 dimensions and that space-time has not gone mad. ;-)

angles for this table base

Attachments

Attachments

Attachments

Top Contributors this Month

Recommended Communities